FAN LAWS EXPLAINED: WATCH OUR NEW VIDEO HERE!
In this video, we review 3 major principles of fan performance called Fan Laws. These 3 Fan Laws explain how a fan’s airflow, pressure, and power consumption change in response to a change in fan operating speed within certain fixed systems. By a fixed system, we mean no variables in the system are changing that would skew the calculations discussed in this video, such as closing a damper or a blast gate. The formulas discussed in this video should be used as general approximations with an understanding that certain equipment, like dust collectors, do not follow fan laws.
Lets start by reviewing some key terms:
- RPM, or, Revolutions Per Minute, quantifies the speed a fan’s wheel rotates.
- CFM, or, Cubic Feet per Minute, is a unit of measurement for the volume of airflow a fan moves as the wheel rotates. Volume is also commonly measured in Cubic Meters per Hour in metric units.
- BHP, or, Brake Horsepower, is a measure of power consumption. Power consumption is commonly measured in Horsepower or Kilowatts.
- SP stands for Static Pressure, and is commonly measured in inches of water gauge. Pressure is also commonly measured in Pascals when using the metric system.
- In the context of HVAC and industrial air movement, static pressure is the resistance to airflow. Because air has mass, it creates friction as a fan moves it through ducting or piping. That friction is resistance that a fan has to overcome to move air through a system. To overcome that resistance, a fan has to generate enough pressure to match the system’s static pressure.
With these concepts in mind, we can define the first three fan laws.
The first fan law describes how airflow changes in response to a change in speed, and the change is a 1 to 1 ratio. This can be conceptualized by thinking of the blades on a wheel as a set of equally sized shovels, each moving an equal amount of matter with each shovel full, or, rotation. By changing the speed, you change the frequency with which each shovel moves an equal amount of matter. In other words, it changes at a 1:1 ratio, which is what the first fan law shows us algebraically. The change in speed, or, new speed divided by old speed, is equal to the change in flow, or, new flow divided by old flow.

As a numeric example, let’s say we have a fan that’s running at 1,000 RPM, moving 10,000 cubic feet per minute while generating 10 inches of water gauge in static pressure, at 100 brake horsepower. In our example, we’ll double the speed, from 1,000 rpm to 2,000 rpm. So, the equation is the new speed, 2,000 RPM, divided by the previous speed, 1,000 RPM, equals the new CFM, X, divided by the old CFM, 10,000, which solves for a new flow of 20,000 CFM.

The second fan law describes how pressure changes in response to a change in speed. The equation is similar to the first fan law, but here the pressure changes as a function of the change in speed squared, meaning pressure is much more sensitive to a change in speed than flow. Mathematically, that’s: the quantity of the change in speed squared equals the change in pressure.

We’ll use the same operating point as our first example, doubling the speed from 1,000 RPM to 2,000 RPM, to see how the 10-inch static pressure changes. The equation is the quantity of 2,000 RPM over 1,000 RPM, squared, equals the new pressure, X, divided by the old pressure, 10, which solves for a new static pressure of 40 inches of water gauge.
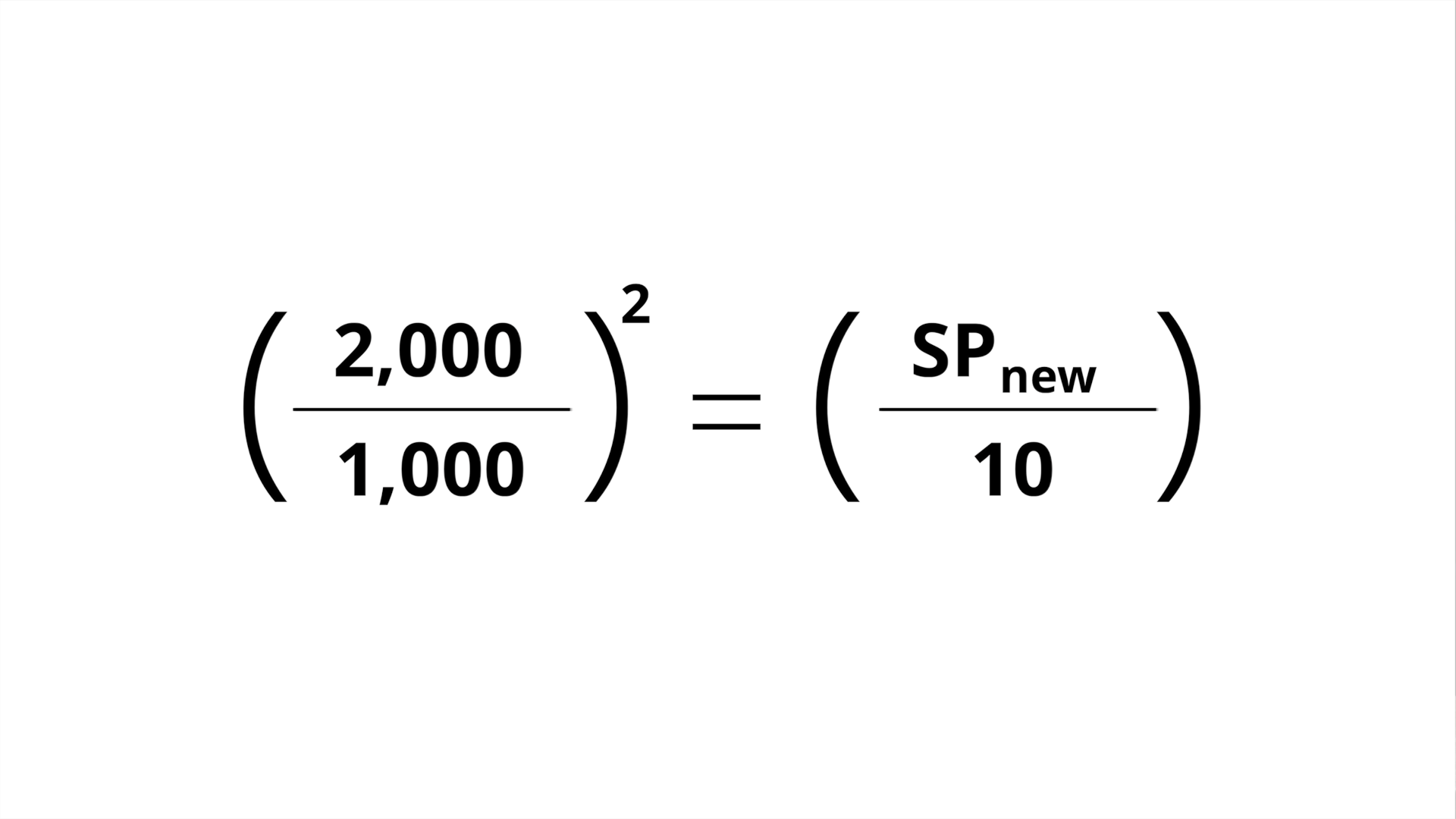
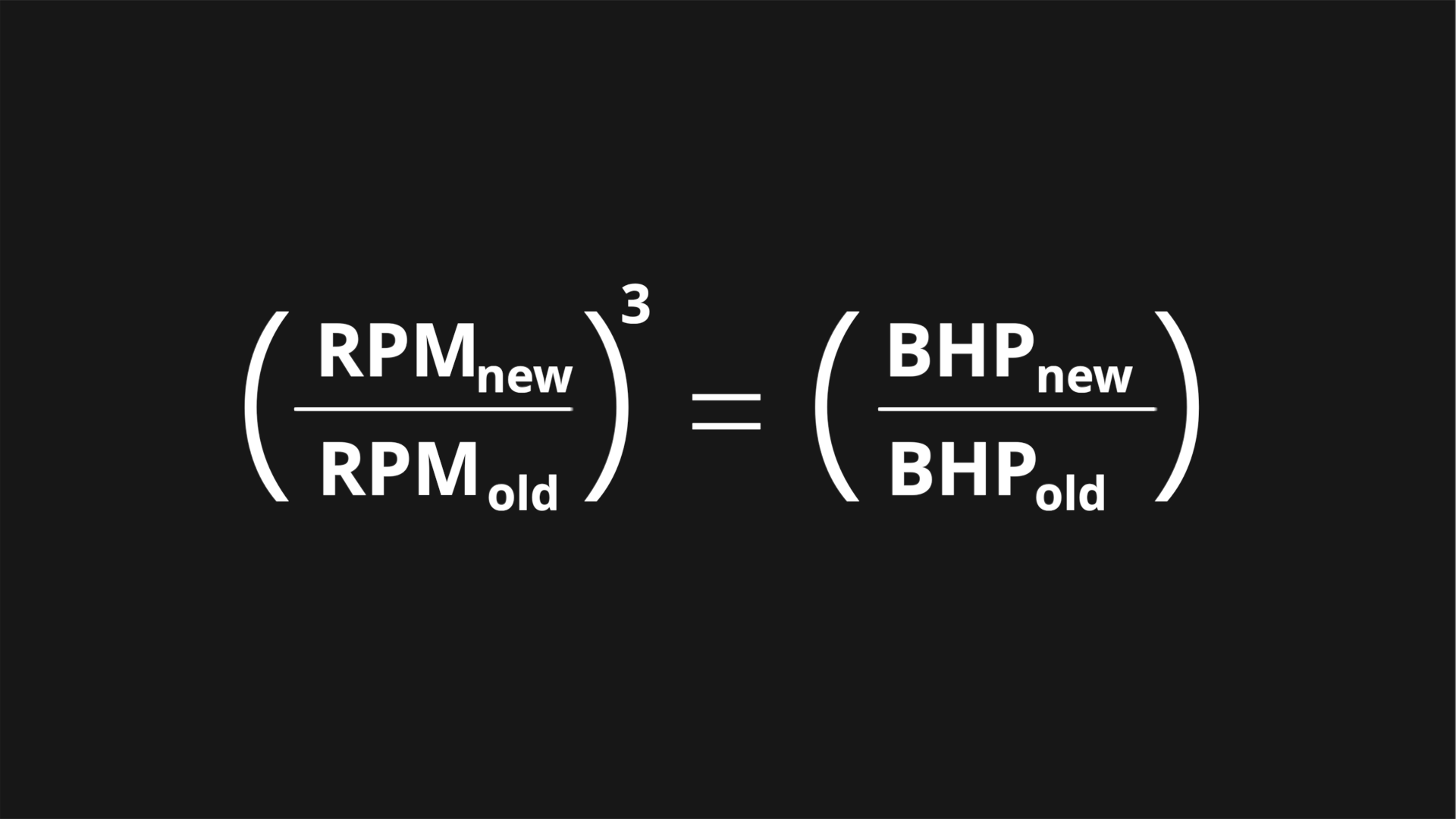
The third fan law describes how brake horsepower changes in response to a change in speed. Another similar setup, but here the horsepower changes as a function of the change in speed cubed. This exponential impact on power consumption is useful in determining how much headroom a fan assembly has for speed increase, before exceeding the motor’s rated capability.
In our example, the equation is, the quantity of 2,000 RPM over 1,000 RPM cubed, equals the new brake horsepower, X, divided by the old brake horsepower, 100, which solves for a new power consumption of 800 BHP.
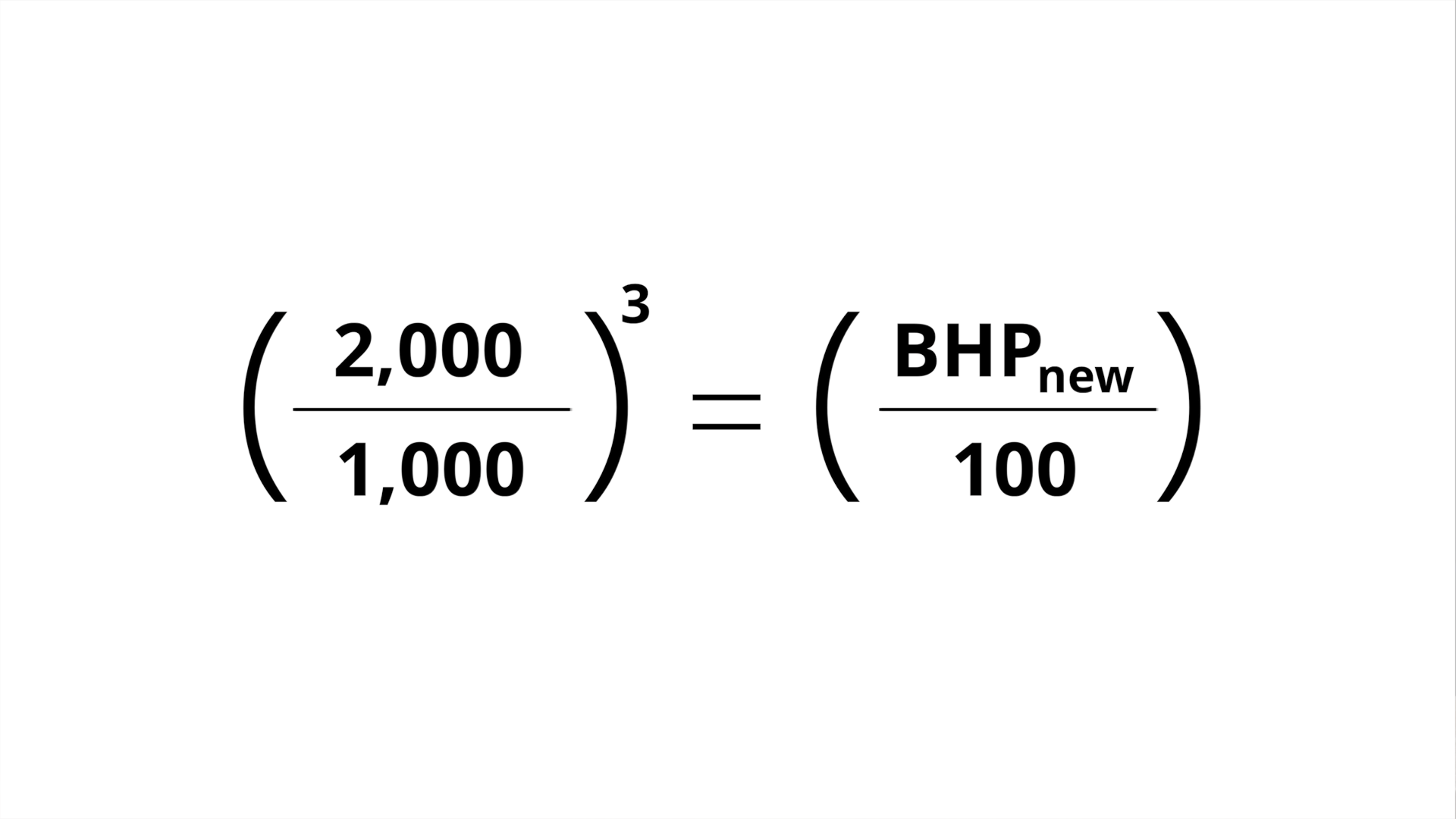
To summarize these 3 fan laws, flow changes proportionately to speed. Static pressure changes as a function of the change in speed squared. And brake horsepower changes as a function of the change in speed cubed. There are other fan laws, but these 3 fundamentals can help you quickly estimate the performance effects of changing speed, either during fan selection, or making changes in the field.

